Manuscripts for my PhD thesis.
| 中文关键词 | English Keywords |
|---|---|
| 舰载直升机 | shipborne helicopter |
| 气动干扰 | aerodynamic interference |
| 旋翼空气动力学 | rotor aerodynamics |
| 间断伽辽金有限元法 | discontinuous Galerkin (DG) finite element method |
| 加权基本无振荡重构 | weighted essentially non-oscillatory (WENO) reconstruction |
| 非定常动量源模型 | unsteady momentum source (UMS) model |
已知函数 \(u(x,y,z)\) 在体单元 \(V_i\) 上的多项式近似:
\[u^{h}|_{V_{i}}(x,y,z)=\sum_{a,b,c}\hat{u}_{a,b,c}(x-x_{0})^{a}(y-y_{0})^{b}(z-z_{0})^{c},\quad(x,y,z)\in V_{i}.\]已知函数 \(u(x,y,z)\) 在非结构网格 \(G\) 上的多项式近似:
\[u^{h}(x,y,z)=\begin{cases} u^{h}|_{V_{1}}(x,y,z), & (x,y,z)\in V_{1},\\ \vdots & \vdots\\ u^{h}|_{V_{i}}(x,y,z), & (x,y,z)\in V_{i},\\ \vdots & \vdots\\ u^{h}|_{V_{N_{V(G)}}}(x,y,z), & (x,y,z)\in V_{N_{V(G)}}. \end{cases}\]函数 \(u(\boldsymbol{r})\) 在体单元 \(V_i\) 的任意一组正交归一化的多项式基
\[\underline{e}(\boldsymbol{r})=\begin{bmatrix}e_{1}(\boldsymbol{r}) & \cdots & e_{n}(\boldsymbol{r})\end{bmatrix}^{t}\]上的投影
\[u^{h}(\boldsymbol{r})=\begin{bmatrix}\langle u\vert e_{1}\rangle_{V_{i}} & \cdots & \langle u\vert e_{n}\rangle_{V_{i}}\end{bmatrix}\begin{bmatrix}e_{1}(\boldsymbol{r})\\ \vdots\\ e_{n}(\boldsymbol{r}) \end{bmatrix}\]是 \(u(\boldsymbol{r})\) 在由 \(\underline{e}(\boldsymbol{r})\) 张成的线性空间中,关于 \(\mathcal{L}_2(V_i)\) 的范数
\[\Vert u-u^{h}\Vert=\left(\int_{V_{i}}|u-u^{h}|^{2}\right)^{1/2}\]最优的多项式近似。
由体单元 \(V_i\) 上的任意一组(完备到 \(p\) 次的)多项式基:
\[\underline{\phi}(\boldsymbol{r}):=\begin{bmatrix}\phi_{1}(\boldsymbol{r}) & \phi_{2}(\boldsymbol{r}) & \cdots & \phi_{n}(\boldsymbol{r})\end{bmatrix}^{t},\qquad n=\binom{p+d}{d},\]总是可以构造出 \(V_i\) 上的一组正交归一化的多项式基:
\[\underbrace{\begin{bmatrix}e_{1}(\boldsymbol{r})\\ e_{2}(\boldsymbol{r})\\ \vdots\\ e_{n}(\boldsymbol{r}) \end{bmatrix}}_{\underline{e}}=\underbrace{\begin{bmatrix}S_{11}\\ S_{21} & S_{22}\\ \vdots & \vdots & \ddots\\ S_{n1} & S_{n2} & \cdots & S_{nn} \end{bmatrix}}_{\underline{S}}\underbrace{\begin{bmatrix}\phi_{1}(\boldsymbol{r})\\ \phi_{2}(\boldsymbol{r})\\ \vdots\\ \phi_{n}(\boldsymbol{r}) \end{bmatrix}}_{\underline{\phi}}.\]定义在区域 \(\Omega\) 上的双曲型微分方程
\[\partial_{t}\underline{U}+\nabla\cdot\underline{\boldsymbol{F}}=\underline{H}\]它等价于
\[\int_{V}\left(\partial_{t}\underline{U}+\nabla\cdot\underline{\boldsymbol{F}}\right)\psi=\int_{V}\psi\,\underline{H}\]在 \(\forall V\subset\Omega\) 上对任意充分光滑的函数 \(\psi\colon\Omega\to\mathbb{R}\) 都成立。
\[\int_{V}\left(\psi\,\partial_{t}\underline{U}-\underline{\boldsymbol{F}}\cdot\nabla\psi\right)+\oint_{\partial V}\psi\,\underbrace{\boldsymbol{\nu}\cdot\underline{\boldsymbol{F}}}_{\underline{F}^{\nu}}=\int_{V}\psi\,\underline{H}\]取一组以 \(V_i\) 为支集、充分光滑的正交归一基函数 \(\left\{ \phi_{k}\right\} _{k=1}^{K}\)
则 \(U\) 与 \(\psi\) 可以分别近似为
\[\underline{U}^{h}(\boldsymbol{r},t)=\sum_{k=1}^{K}\underline{\hat{U}}_{k}(t)\,\phi_{k}(\boldsymbol{r}),\qquad \psi^{h}(\boldsymbol{r})=\sum_{k=1}^{K}\hat{\psi}_{l}\,\phi_{k}(\boldsymbol{r})\]将其代入弱形式,并利用 \(\psi\) 的任意性,即得常微分方程组
\[\left(\frac{\mathrm{d}}{\mathrm{d}t}\underline{\hat{U}}\right)\begin{bmatrix}\langle\phi_{1}\vert\phi_{1}\rangle_{V_{i}} & \cdots & \langle\phi_{1}\vert\phi_{K}\rangle_{V_{i}}\\ \vdots & \ddots & \vdots\\ \langle\phi_{K}\vert\phi_{1}\rangle_{V_{i}} & \cdots & \langle\phi_{K}\vert\phi_{K}\rangle_{V_{i}} \end{bmatrix}=\underline{R}_{V_{i}}-\underline{R}_{\partial V_{i}},\qquad\forall V_{i}\in V_{G(\Omega)}\]一阶即显式欧拉推进:
\[\underline{\hat{U}}^{n+1} =\underline{\hat{U}}^{n}+h_{t}\underline{\hat{R}}^{n}.\]常用的是三步三阶:
\[\begin{aligned}\underline{\hat{U}}^{n+1/3} & =\underline{\hat{U}}^{n}+h_{t}\underline{\hat{R}}^{n},\\ \underline{\hat{U}}^{n+2/3} & =\frac{3}{4}\underline{\hat{U}}^{n}+\frac{1}{4}\left(\underline{\hat{U}}^{n+1/3}+h_{t}\underline{\hat{R}}^{n+1/3}\right),\\ \underline{\hat{U}}^{n+1}\equiv\underline{\hat{U}}^{n+3/3} & =\frac{1}{3}\underline{\hat{U}}^{n}+\frac{2}{3}\left(\underline{\hat{U}}^{n+2/3}+h_{t}\underline{\hat{R}}^{n+2/3}\right). \end{aligned}\]桨叶穿过四面体单元的几种常见情形:
含动量源的三维欧拉方程可以写成
\[\partial_{t}\begin{bmatrix}\rho\\ \rho\boldsymbol{u}\\ \rho e_{0} \end{bmatrix}+\nabla\cdot\begin{bmatrix}\rho\boldsymbol{u}\\ \rho\boldsymbol{u}\boldsymbol{u}\\ \rho h_{0}\boldsymbol{u} \end{bmatrix}=\begin{bmatrix}0\\ {\color{red}\boldsymbol{b}_{\mathrm{V}}}-\nabla p\\ {\color{red}\boldsymbol{b}_{\mathrm{V}}\cdot\boldsymbol{u}} \end{bmatrix},\]其中,\(\boldsymbol{b}_{\mathrm{V}}\) 为单位体积气体所受到的外力。
体积分化为线积分:
\[\int_{V_{i}}\phi_{k}(\boldsymbol{r})\,\boldsymbol{b}_{\mathrm{V}}(\boldsymbol{r})=\int_{\overline{RS}}\phi_{k}(\boldsymbol{r})\,\boldsymbol{b}_{\mathrm{L}}(\boldsymbol{r}).\]外力线密度:
\[\boldsymbol{b}_{\mathrm{L}}(\boldsymbol{r}(s))=-\begin{bmatrix}\boldsymbol{e}_{L}(s) & \boldsymbol{e}_{D}(s)\end{bmatrix} \begin{bmatrix}C_{L}(\alpha,M)\\ C_{D}(\alpha,M) \end{bmatrix} \rho c\frac{u^{2}+w^{2}}{2}\]可压缩流场的三种典型间断:
| 激波 | 接触间断 | 膨胀波 |
|---|---|---|
即使没有激波,桨叶上下表面之间的压强差也属于强间断!
例:阶跃函数的 DG3 近似在间断附近发生数值振荡:
以本单元及面相邻单元的多项式为候选多项式:
\[u_{k\to i}(\boldsymbol{r}):= u_{k}(\boldsymbol{r})-\langle u_{k}\rangle_{i}+\langle u_{i}\rangle_{i}\]计算各候选多项式的光滑度:
\[\beta_{k\to i}=\sum_{\vert\alpha\vert=1}^{p}\frac{\vert V_{i}\vert^{2\vert\alpha\vert/\color{red}{3}}-1}{(\vert\alpha\vert!)^{2}}\int_{V_{i}}\left(\frac{\partial^{\vert\alpha\vert}u_{k\to i}}{\partial x^{\alpha_{x}}\partial y^{\alpha_{y}}\partial z^{\alpha_{z}}}\right)^{2}\]计算各候选多项式的非线性权重:
\[w_{k\to i}=\frac{w_{k\to i}^{\beta}}{\sum_{k\in K_{i}}w_{k\to i}^{\beta}} ,\qquad w_{k\to i}^{\beta}=\frac{w_{k\to i}^{\star}}{\left(10^{-6}+\beta_{k\to i}\right)^{2}}\]以候选多项式的凸组合为重构的多项式:
\[u_{i}^{\mathrm{new}}(\boldsymbol{r})=\sum_{k\in K_{i}}w_{k\to i}\,u_{k\to i}(\boldsymbol{r})\]| 方案 | 结果 |
|---|---|
| 不加限制器 | |
| 加密 \(h\downarrow\) | |
| 升阶 \(p\uparrow\) |
| 一阶 | 三阶 | |
|---|---|---|
| 云图 | 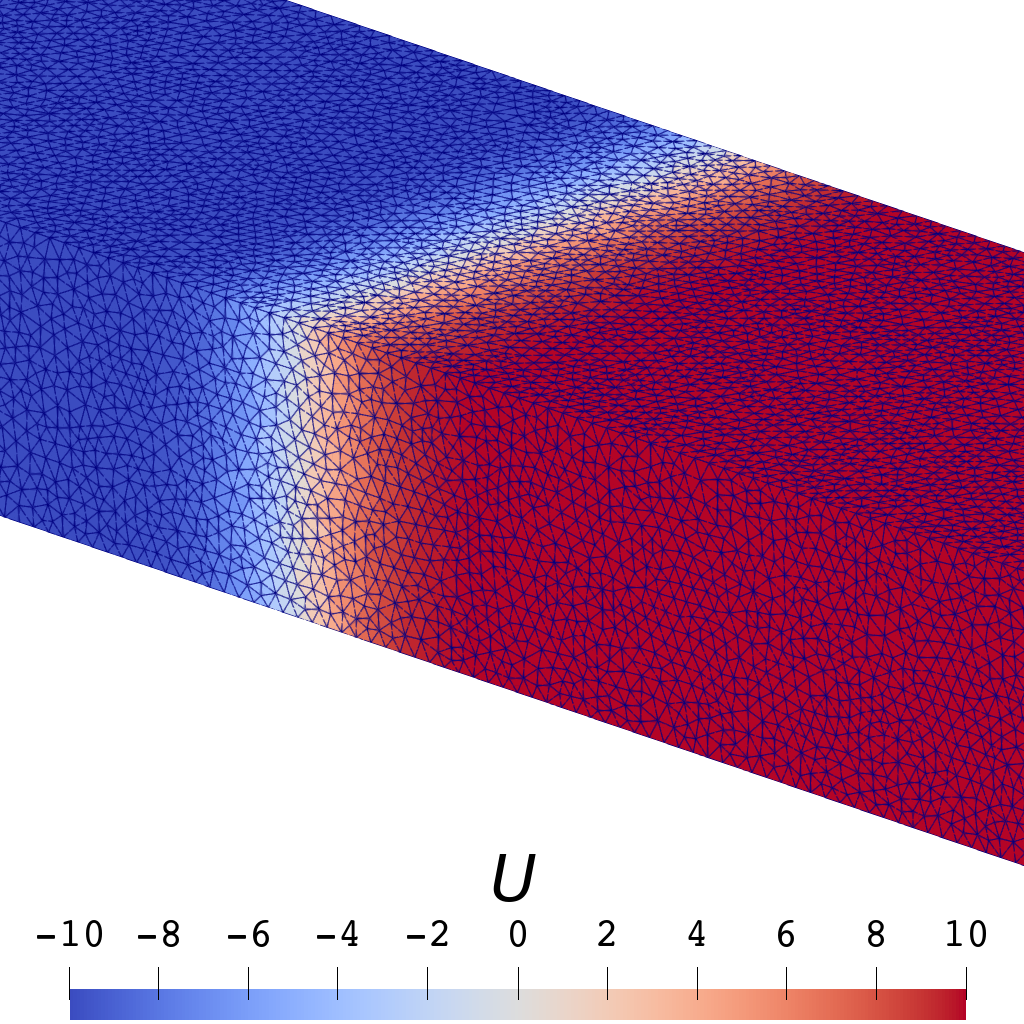 | 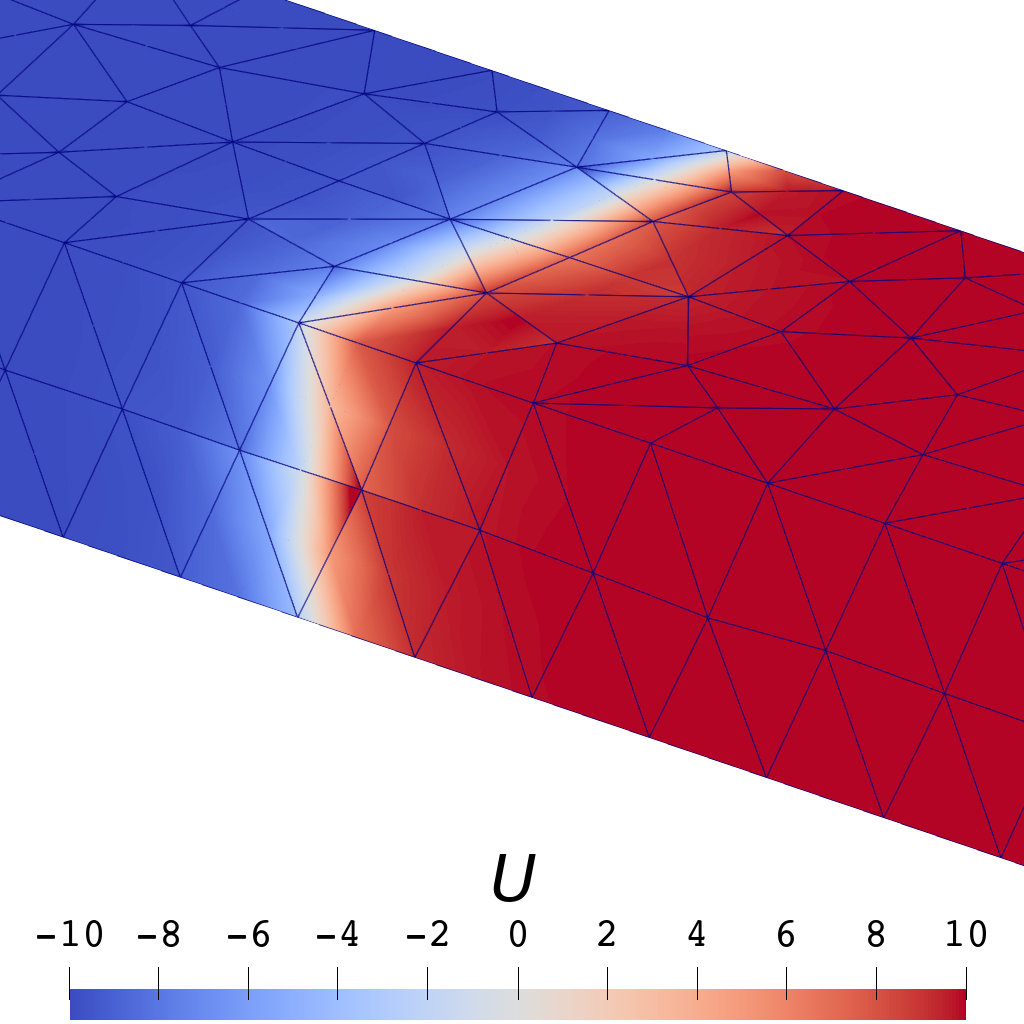 |
| 单元尺寸 | \(2^{-5}\) | \(2^{-2}\) |
| 计算时间 | \(306.3\) | \(4.147\) |
| \(L_1\) 误差 | \(1.108\) | \(1.021\) |
| Sod | Lax | |
|---|---|---|
| 云图 | 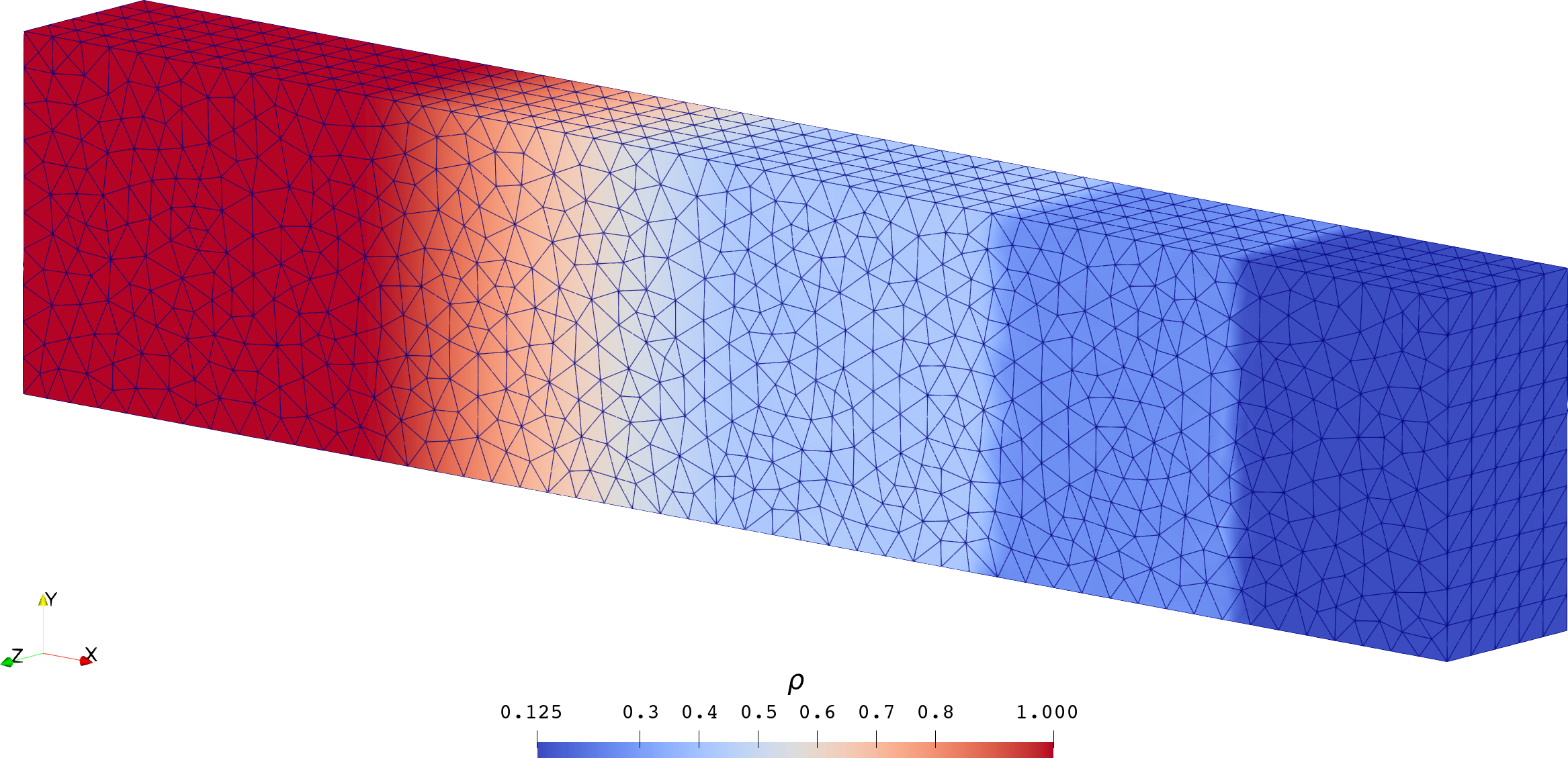 | 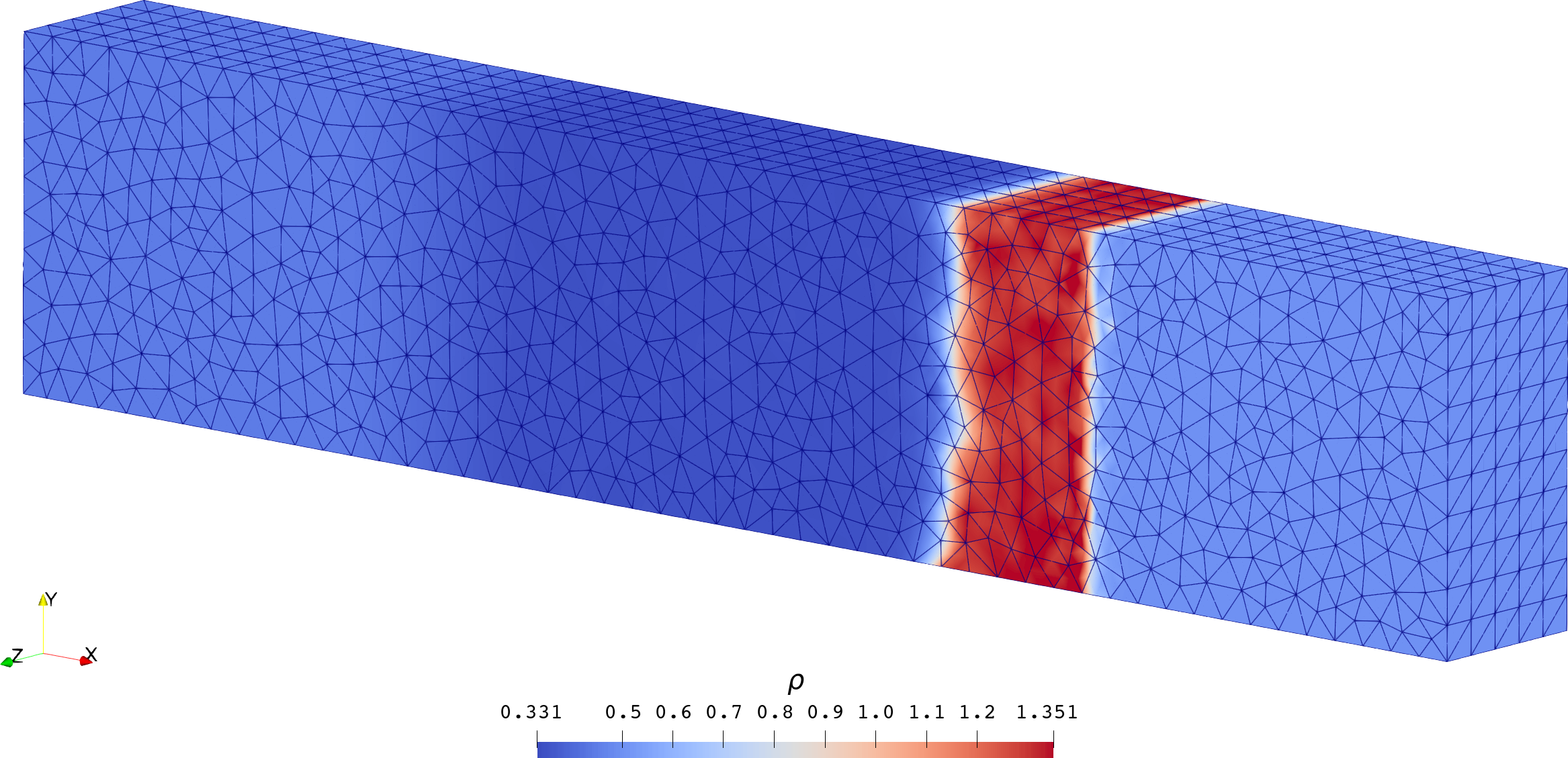 |
| 线图 |
| 方案 | 结果 |
|---|---|
| 时空一阶 | 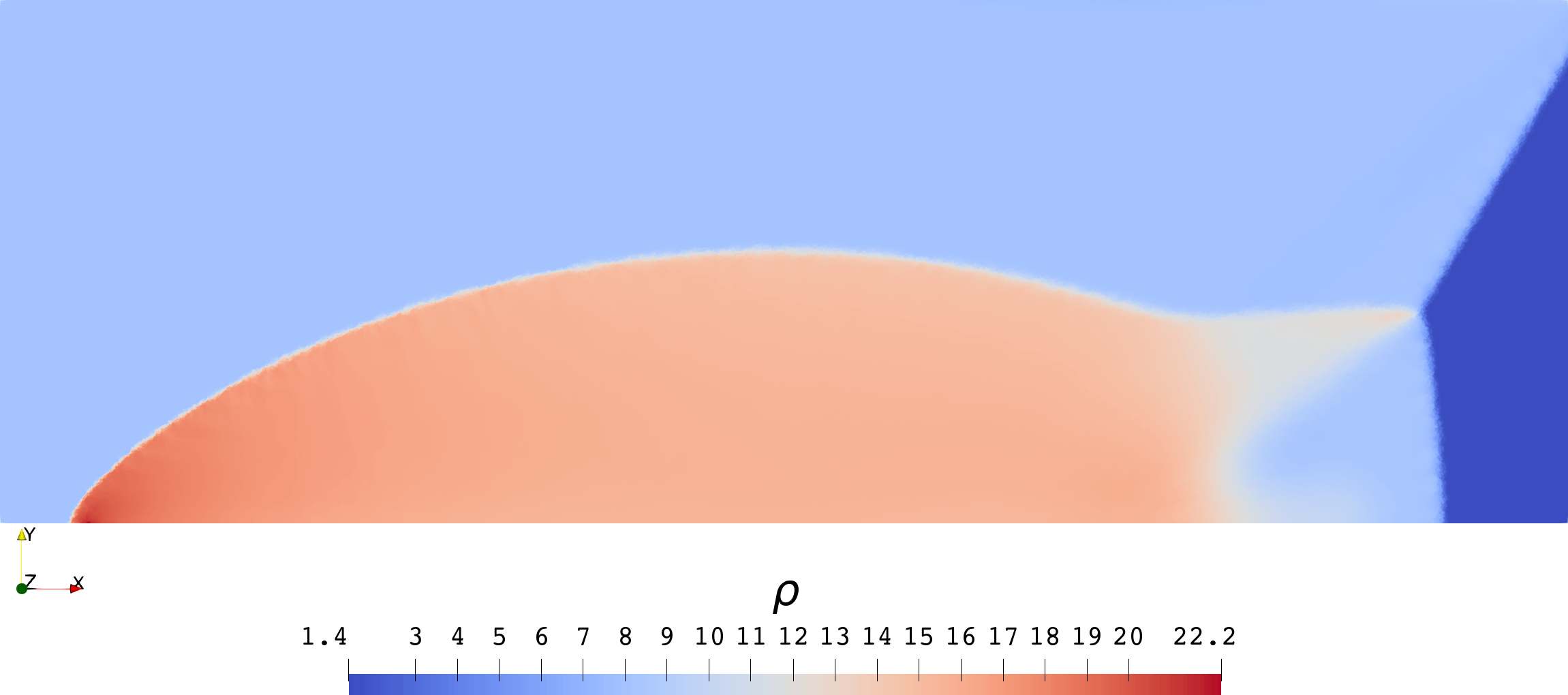 |
| 时空二阶 | 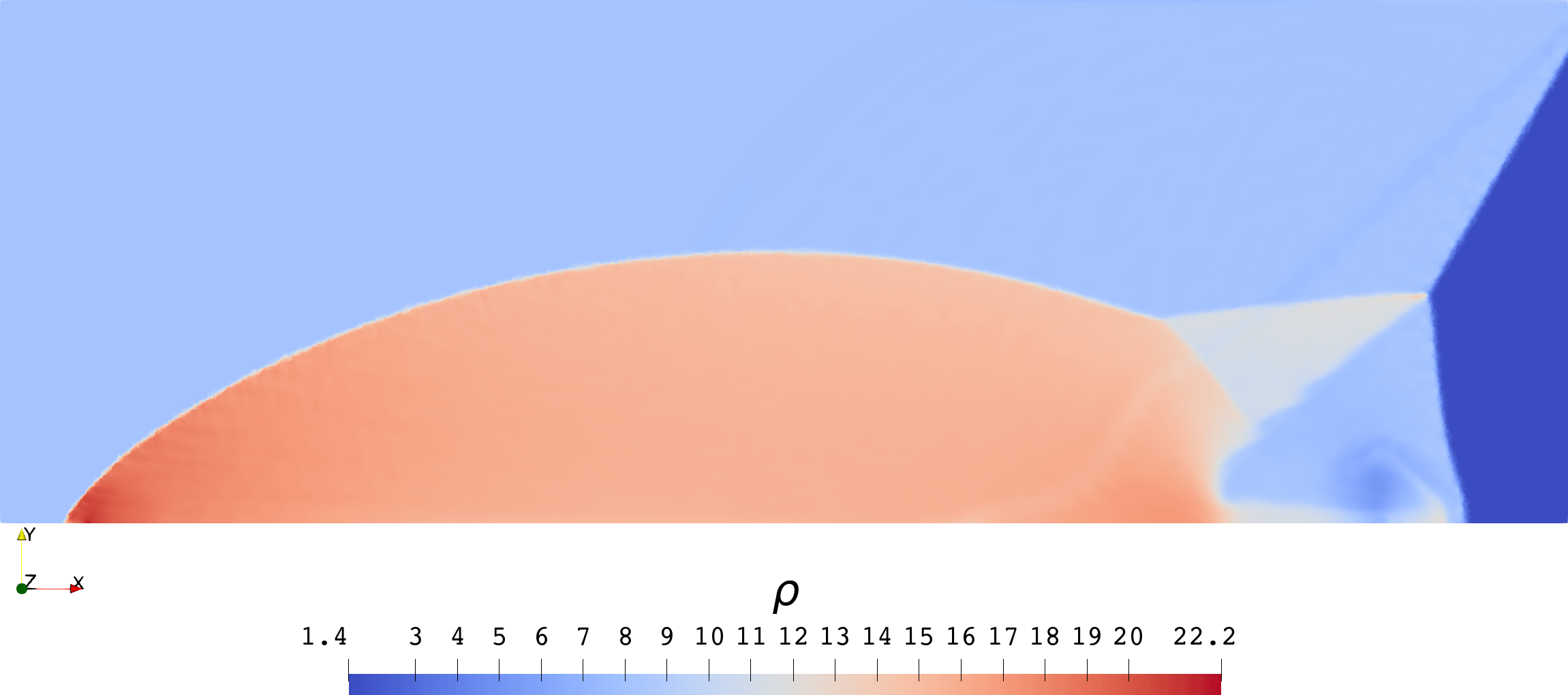 |
| 时空三阶 |  |
| Zhong (2013) | 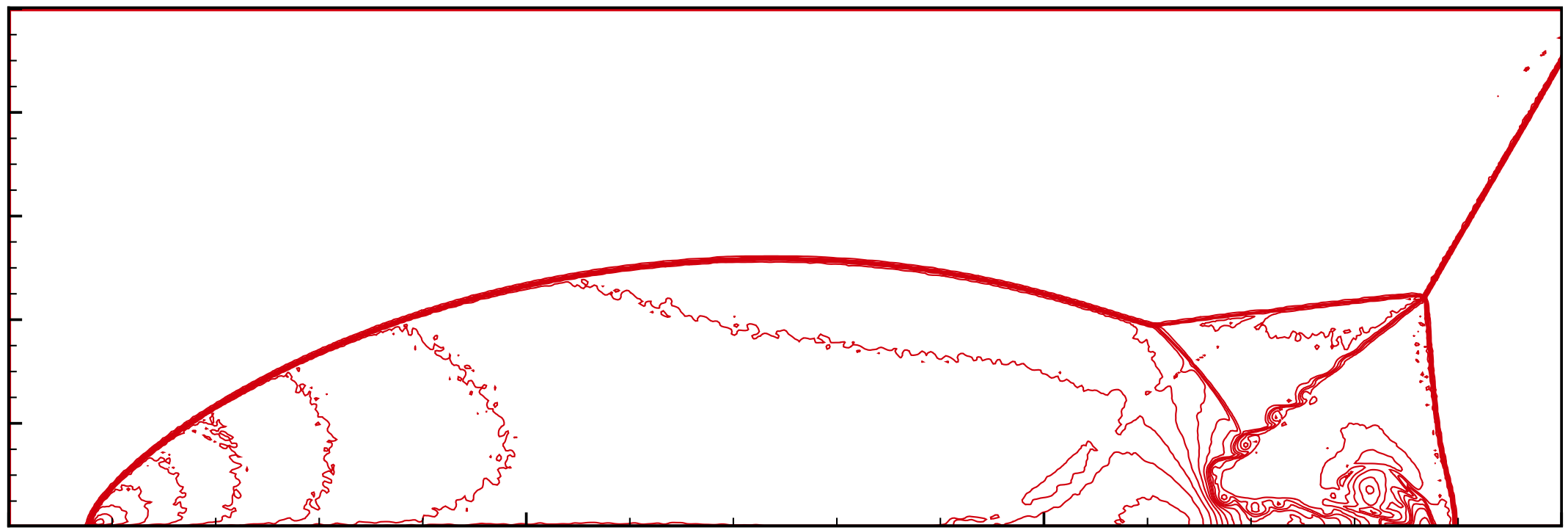 |
| 方案 | 结果 |
|---|---|
| 时空三阶 | 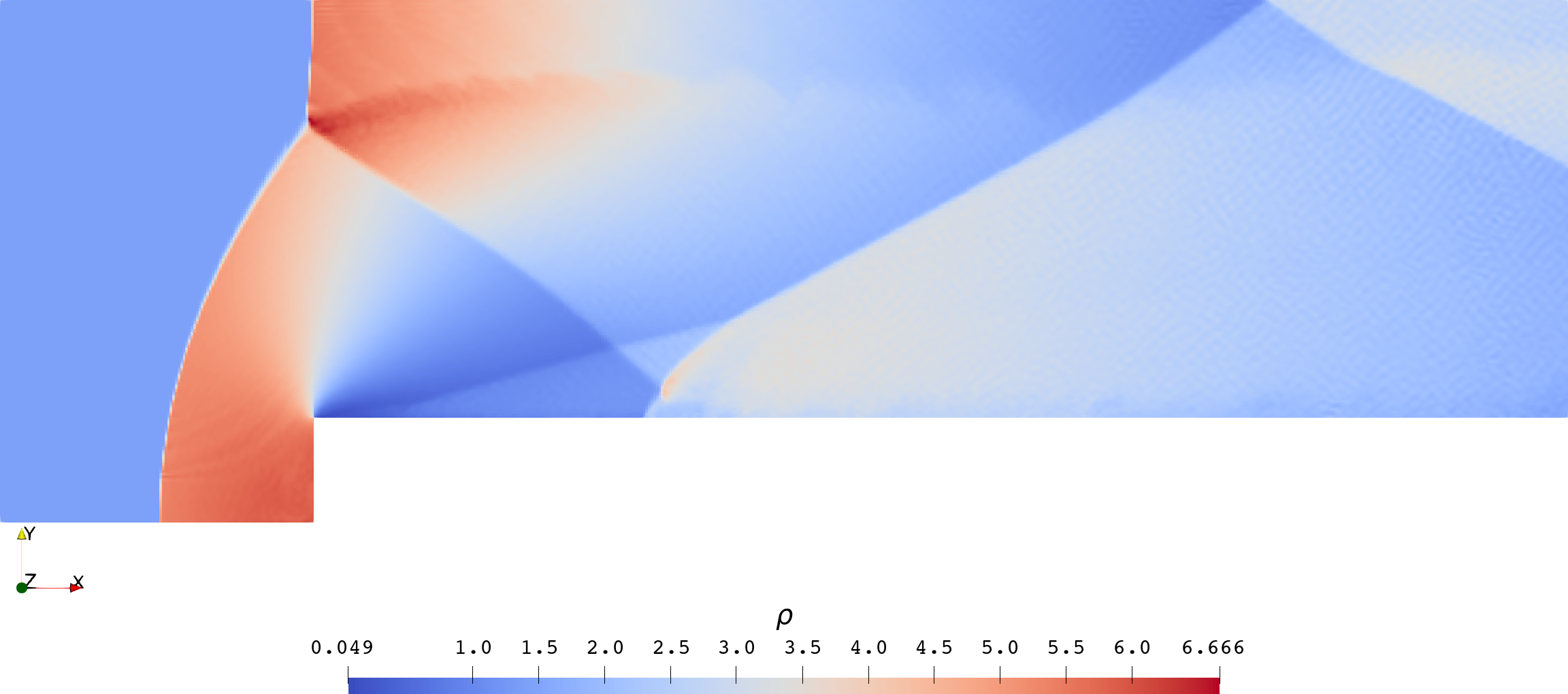 |
| Giri (2019) | 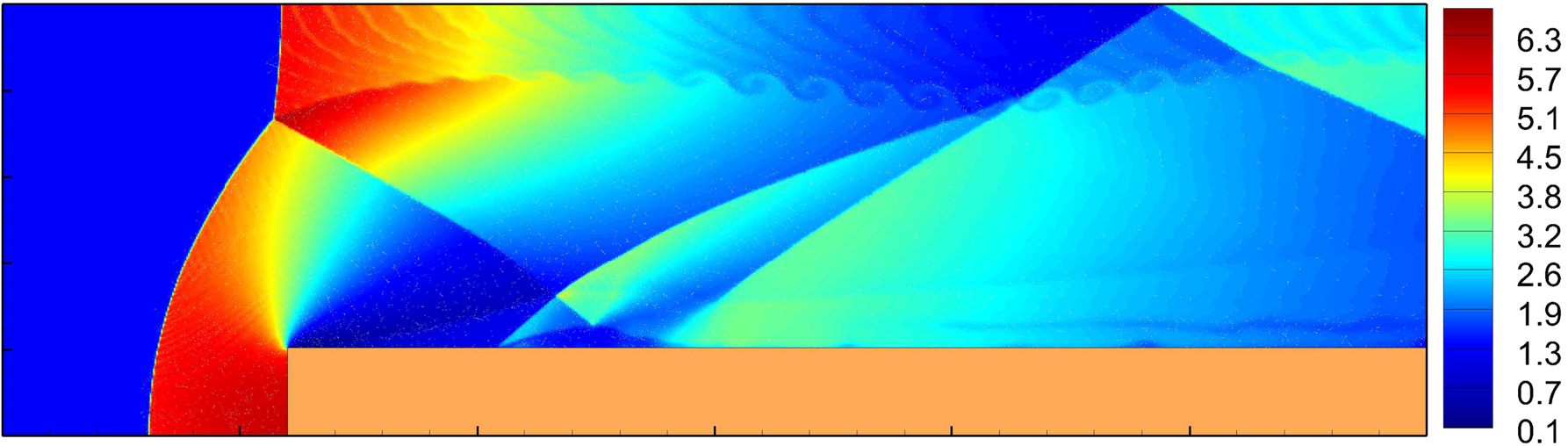 |
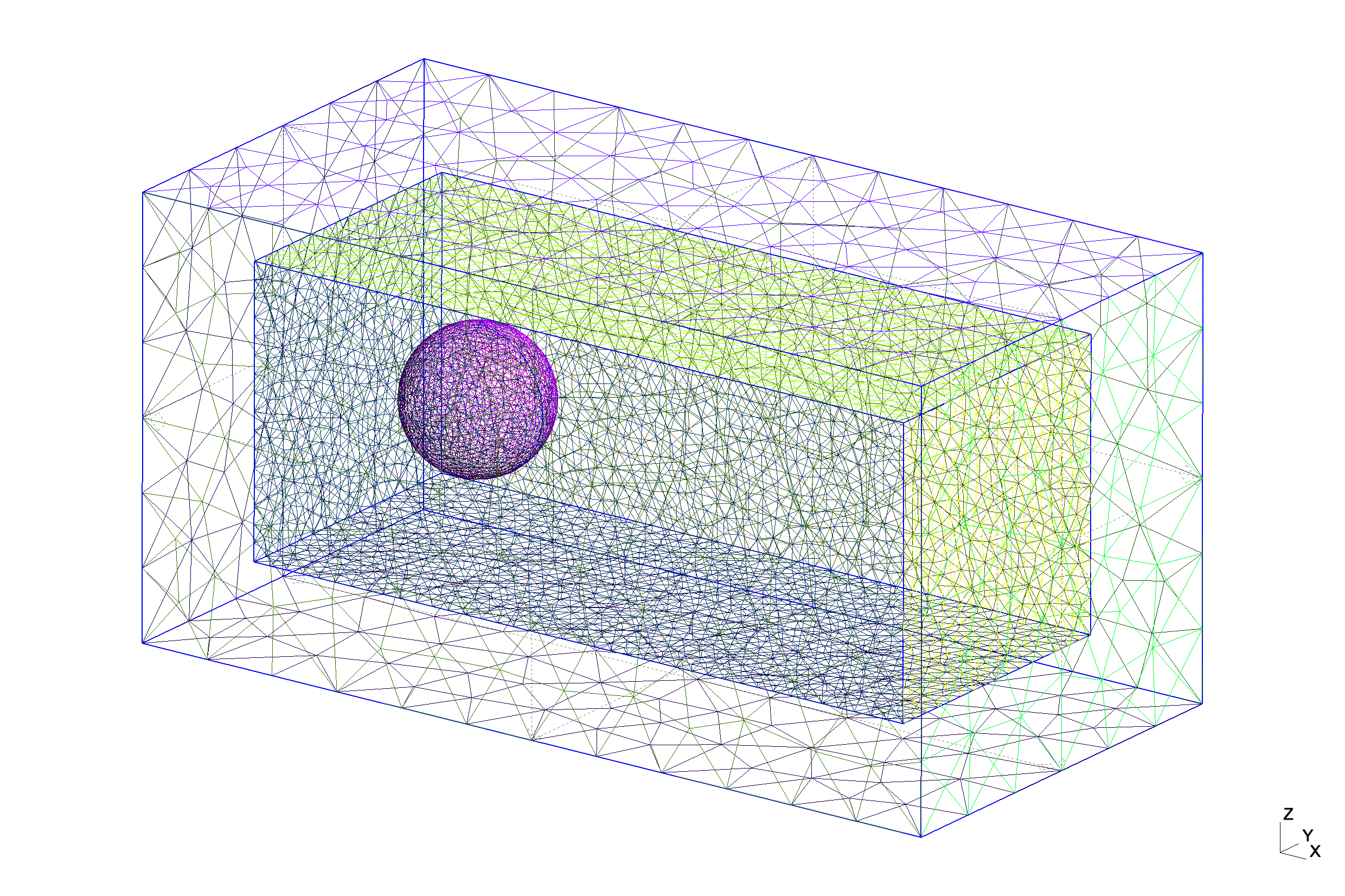
计算网格:
| 方案 | 爬升 | 前飞 |
|---|---|---|
| 时空一阶 |  |  |
| 时空三阶 | 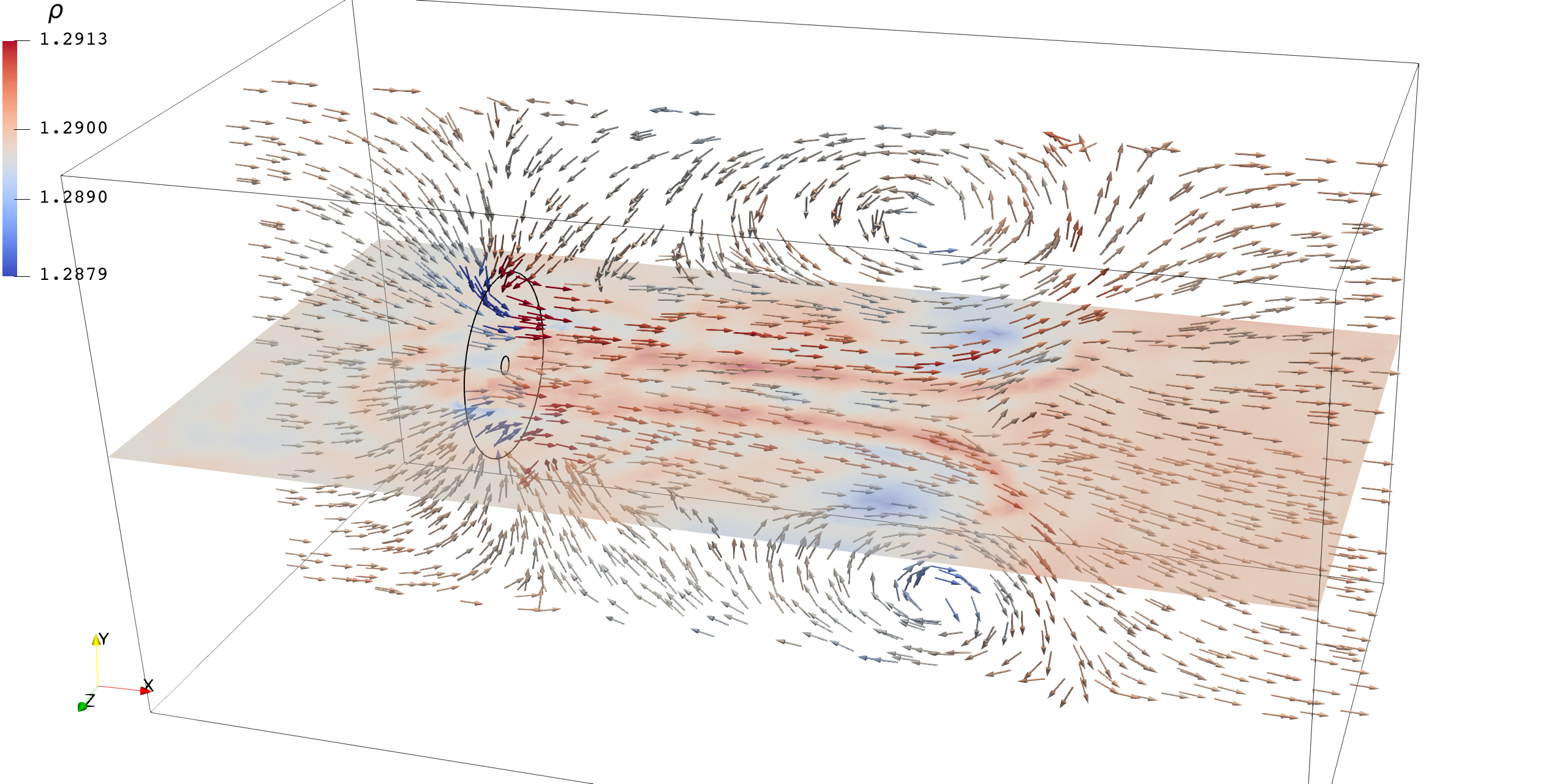 | 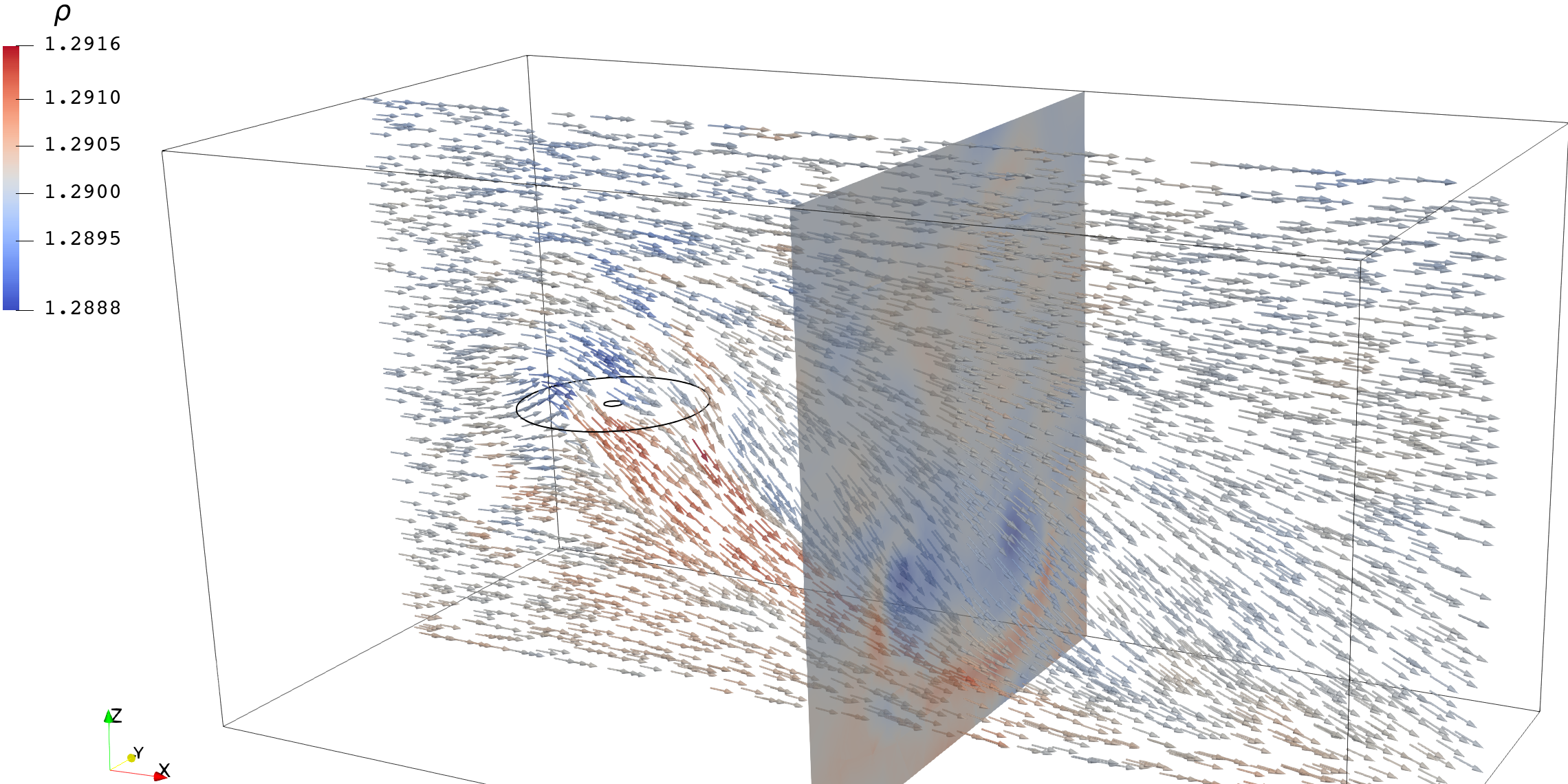 |
用 METIS 对非结构网格分块:
| 双马赫反射 | 孤立旋翼爬升 |
|---|---|
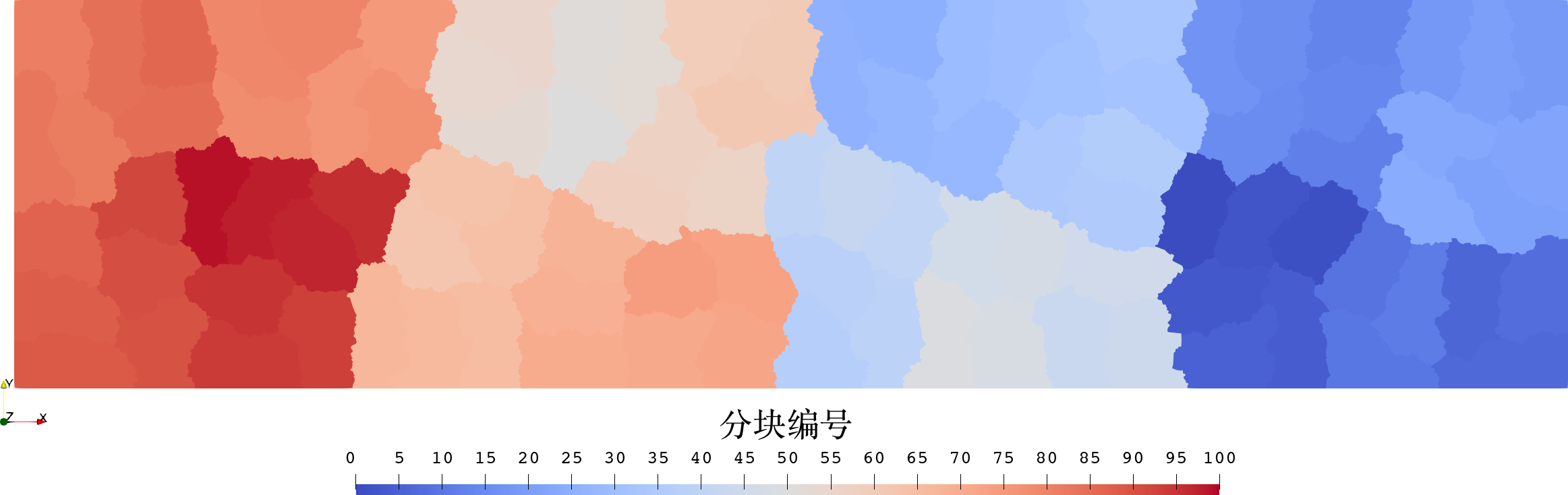 | 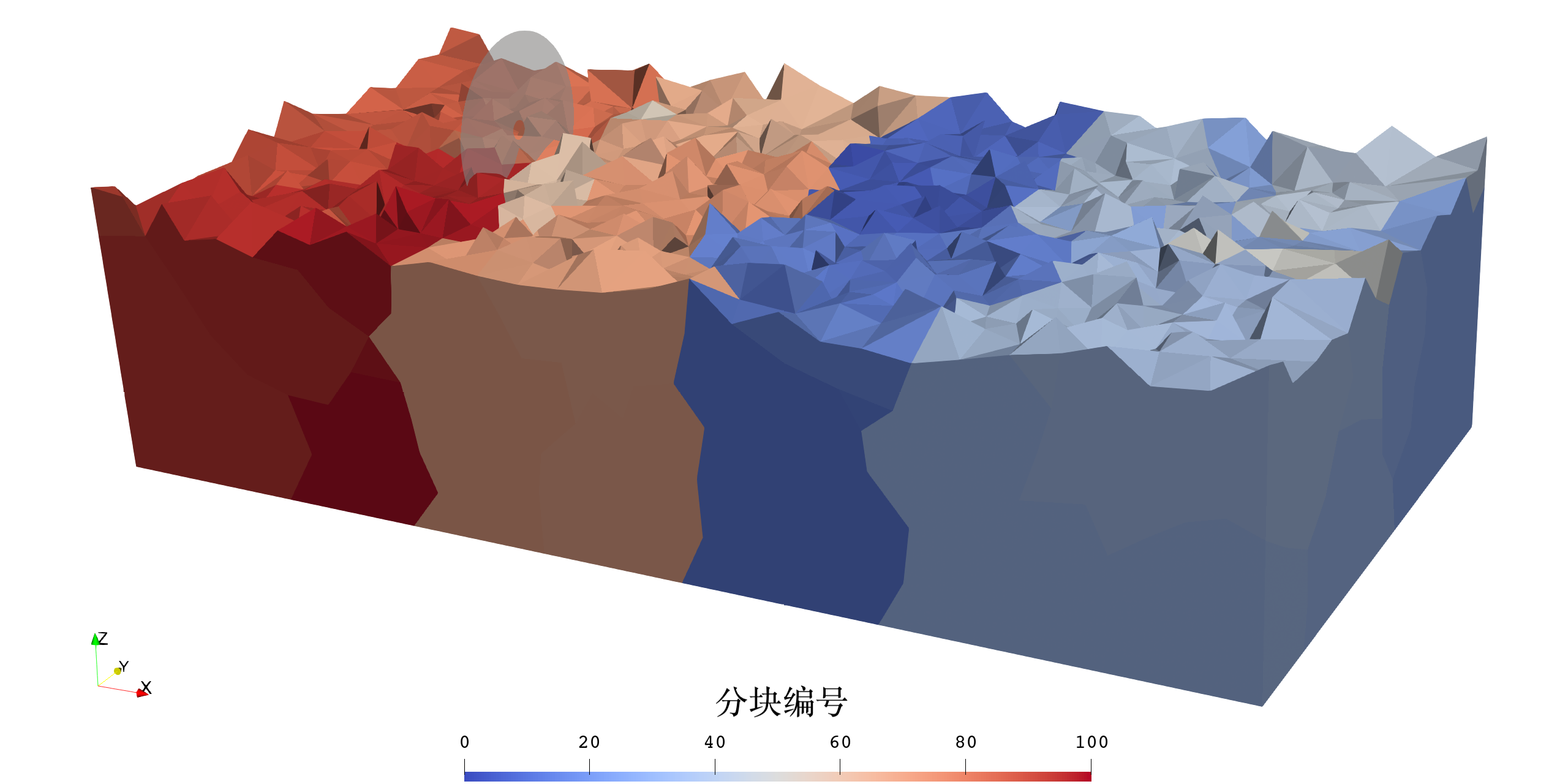 |
各进程单元数量的波动小于 \(3\%\),大致满足负载均衡:
| 双马赫反射 | 孤立旋翼爬升 |
|---|---|
加速比 \(S=\dfrac{T_1}{T_P}\) 实测值:
| 双马赫反射 | 孤立旋翼爬升 |
|---|---|
并行效率 \(E=\dfrac{S}{P}=\dfrac{T_1}{PT_P}\) 实测值:
| 双马赫反射 | 孤立旋翼爬升 |
|---|---|
本章利用上述经过验证的 UMS–RK3/DG3 并行求解器,对一种舰载直升机典型工况下的旋翼–船体–海面气动干扰过程的进行模拟。
该典型工况改编自 Kääriä (2012),几何参数引自 Thedin (2020)。
| 几何参数 | 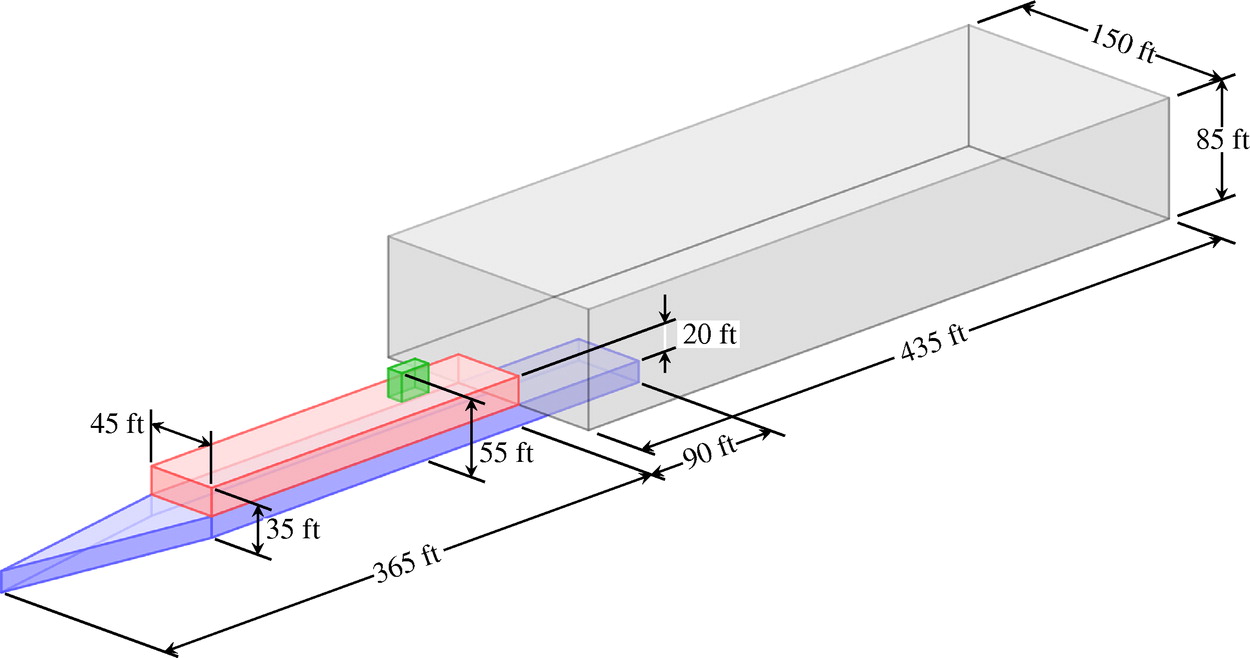 |
| 计算网格 | 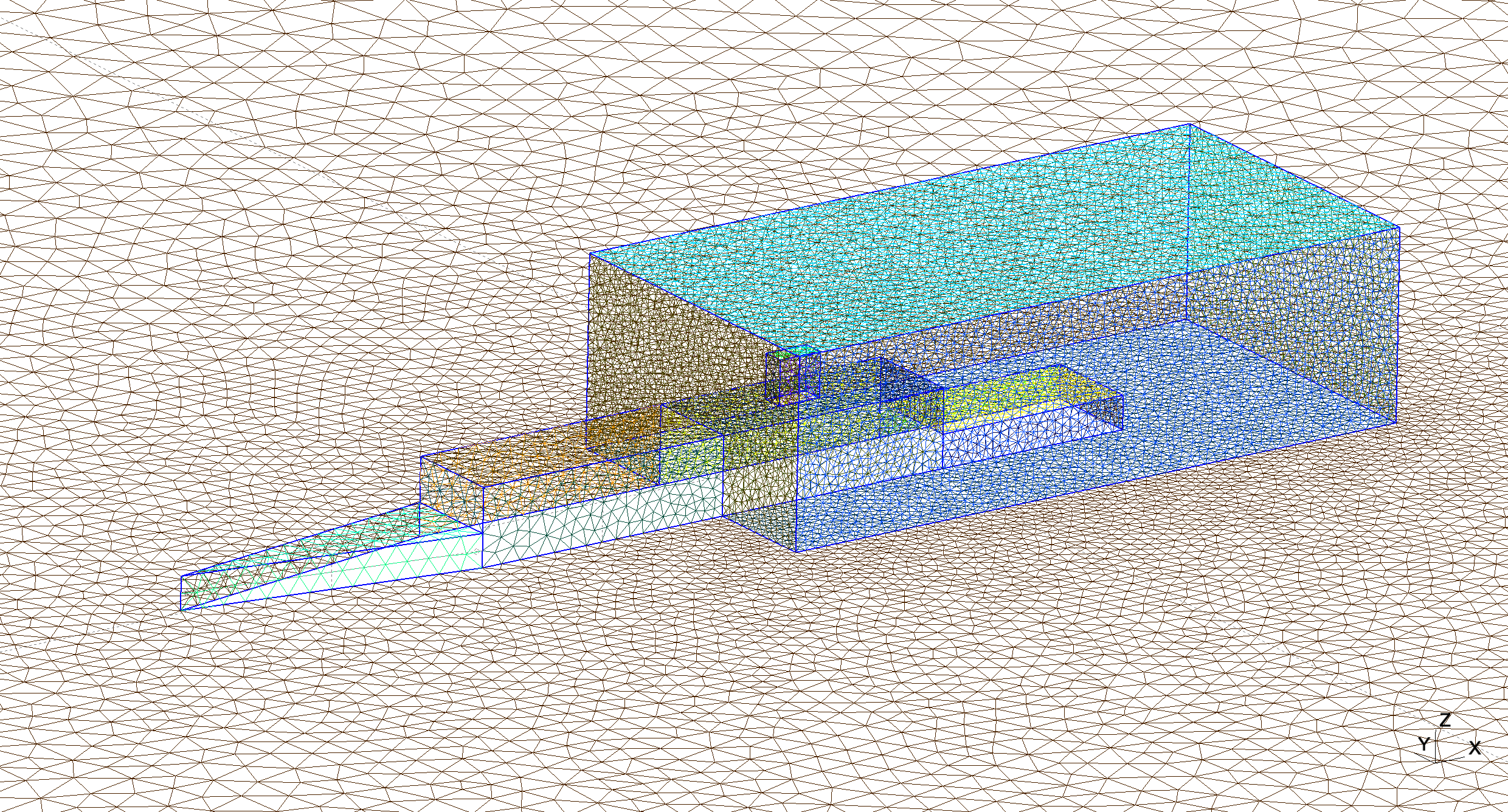 |
除悬停于甲板尾部上方一小节外,旋翼中心均固定于点 \((-45\,\mathrm{ft}, 22.5\,\mathrm{ft}, 40\,\mathrm{ft})\) 处。
起动涡在旋翼后缘形成,并随来流向后(右)运动,运动轨迹大致对应旋翼尾迹后缘。
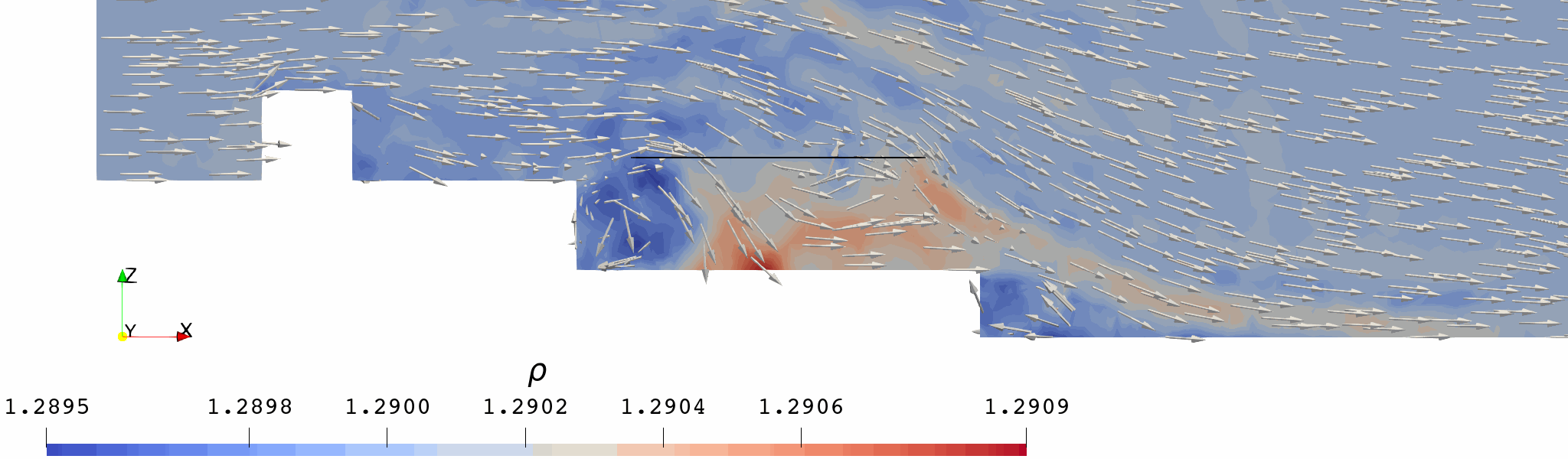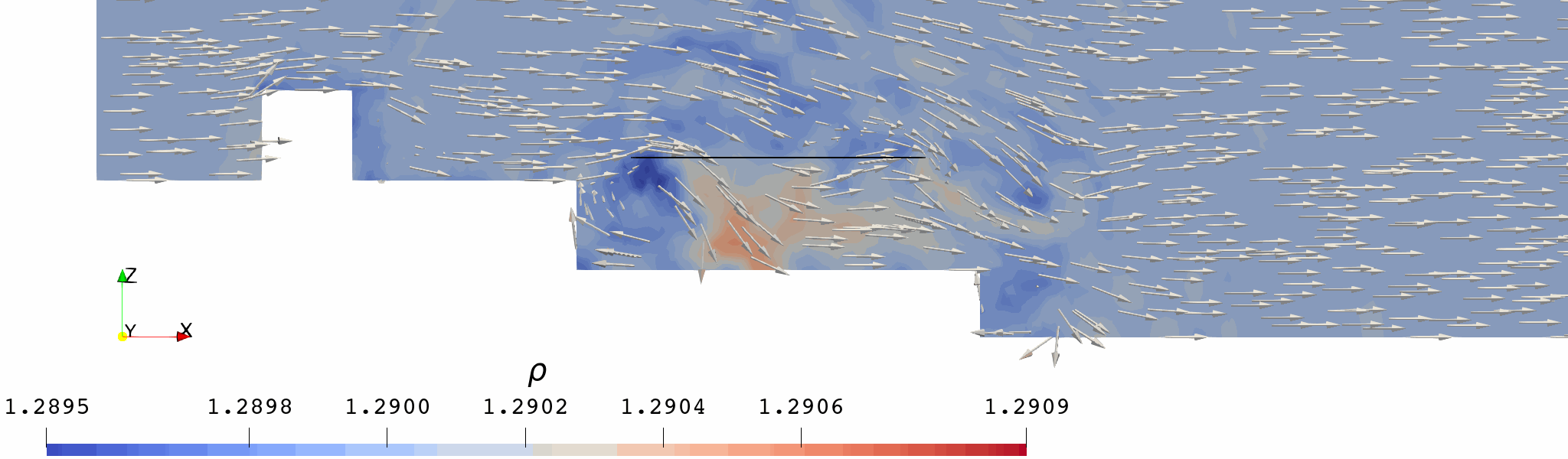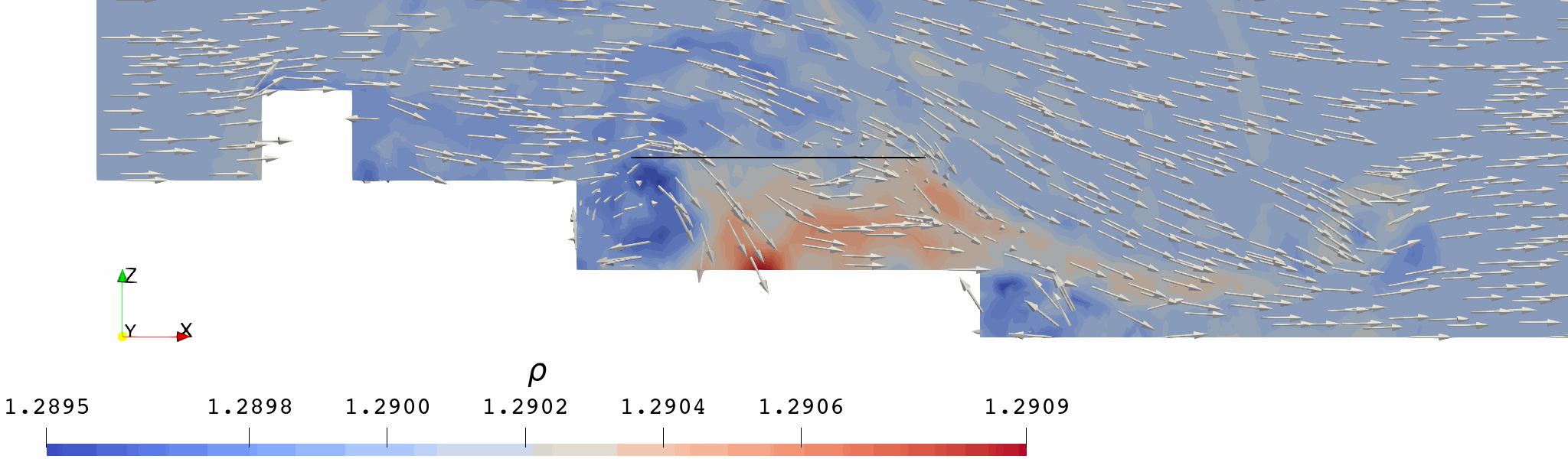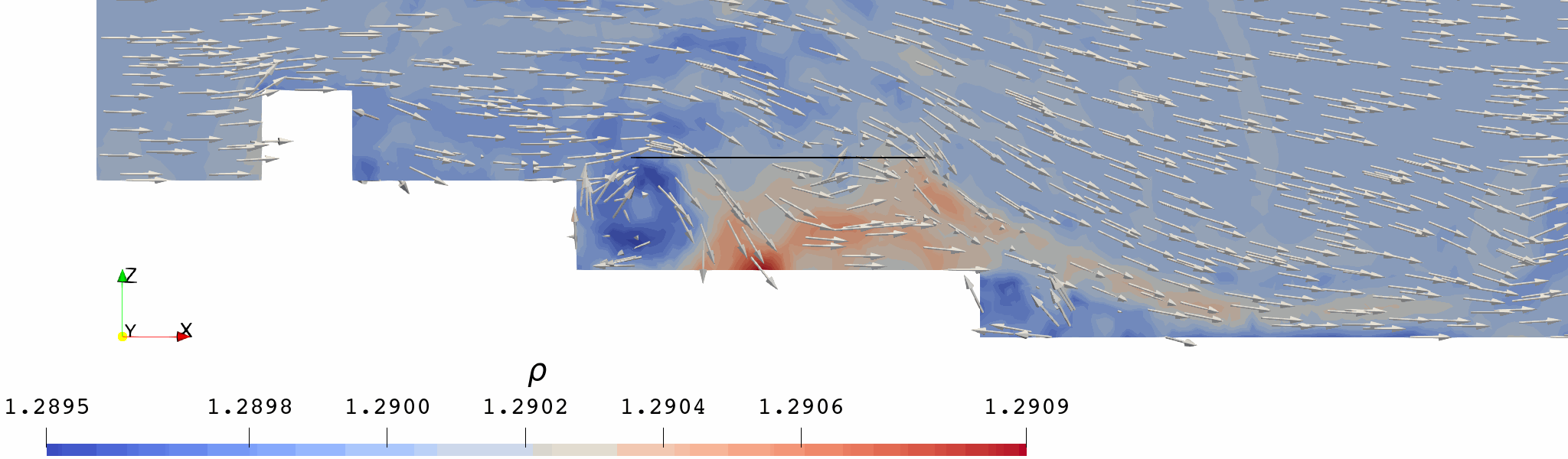


旋翼尾迹具有明显的非对称性:
造成这种差异的主要原因在于船体两侧的气流不对称:

本文提出的 UMS–RKDG 求解器是模拟旋翼流场、研究舰载直升机气动干扰的一种高效、高精度的计算方法。
提出、实现并验证了一种