
按『个人 Wiki』风格整理的学习笔记
template <class Vertex>
struct StaticGraph {
List<List<Vertex>> neighbors;
};
template <class Vertex>
struct DynamicGraph {
Map<Vertex, Set<Vertex>> neighbors;
};
template <class Vertex>
struct ImplicitGraph {
List<Vertex> const& GetNeighbors(Vertex const&);
};
def breadth_first_search(graph, source):
vertex_to_parent = {source: None}
vertex_to_level = {source: 0}
current_level = 0
this_level = [source]
while len(this_level):
next_level = []
for u in this_level:
for v in graph.get_neighbors(u):
if v not in vertex_to_level:
vertex_to_level[v] = current_level
vertex_to_parent[v] = u
next_level.add(v)
this_level = next_level
current_level += 1
return vertex_to_parent, vertex_to_level
Complexity:
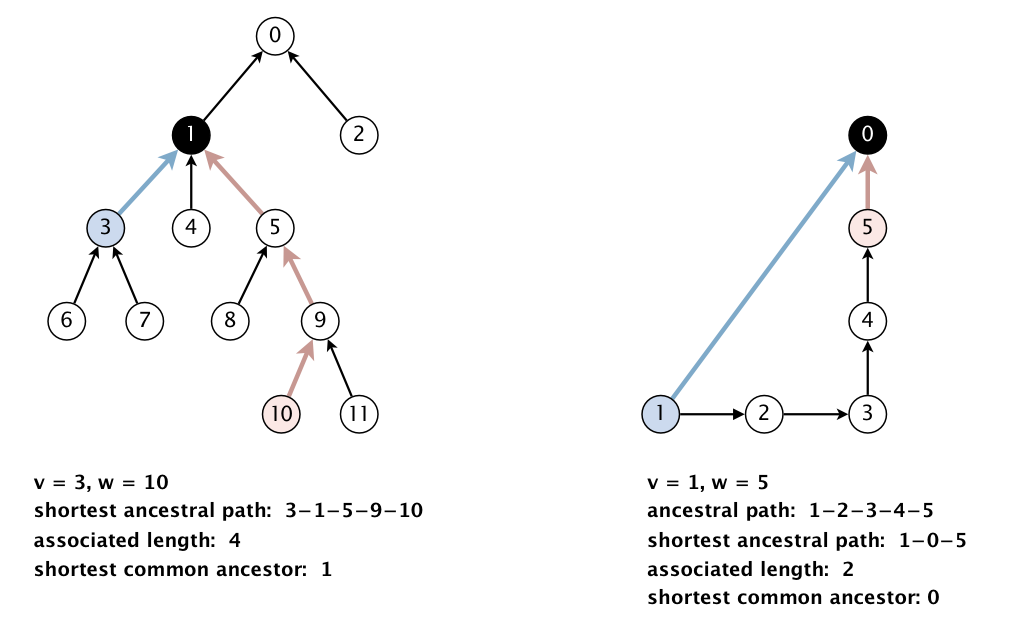
def find_shortest_ancestral_path(graph, u, v):
u_tree = build_bfs_tree(graph, u) # Θ(V + E)
v_tree = build_bfs_tree(graph, v) # Θ(V + E)
d_min = int('inf')
ancestor = None
for x in u_tree: # at most V steps
if x not in v_tree: # Θ(1)
continue
d = u_tree.get_depth(x) + v_tree.get_depth(x): # Θ(1)
if d_min > d: # Θ(1)
d_min = d
ancestor = x
return d_min, ancestor
Complexity:
允许从 i 跳到合法的 i + 1、i - 1 及 a[k] == a[i] 的 k, 求:从 0 到 n - 1 至少需要跳几次?
def depth_first_search(graph):
vertex_to_parent = dict()
for source in graph.vertices:
if source not in vertex_to_parent:
_depth_first_visit(graph, source, vertex_to_parent)
return vertex_to_parent
def _depth_first_visit(graph, source, vertex_to_parent):
for v in graph.get_neighbors(source):
if v not in vertex_to_parent:
vertex_to_parent[v] = source
_depth_first_visit(graph, v, vertex_to_parent)
Complexity:
Edge Classification:
Theorem. Graph has a cycle $\iff$ DFS has a back edge.
DAG: Directed Acylic Graph.
_depth_first_visit() finishes.graphlib.TopologicalSorter provides functionality to topologically sort a graph of hashable nodes.允许从 i 跳到合法的 i + a[i] 或 i - a[i], 求:是否能从 0 跳到某个 a[k] == 0 的 k?
If negative weight edges are present, the algorithm should find negative weight cycles.
Problem. Given an undirected graph $G = (V,E)$ and edge weights $W\colon E\to \mathbb{R}$, find a spanning tree $T$ that minimizes $\sum_{e\in T}W(e)$.
Definition. The contraction of an edge $e\coloneqq{u,v}$ in a graph $G$ is to merge the vertices connected by $e$ and create a new vertex. The new graph is denoted as $G/e$.
Lemma (Optimal Substructure). Suppose $e\coloneqq{u,v}$ is an edge of some MST of $G$. If $T’$ is an MST of $G/e$, then $T’\cup{e}$ is an MST of $G$.
Lemma (Greedy Choice). For any cut $(S,V\setminus S)$ in a weighted graph $G=(V,E,W)$, any least-weight crossing edge $e\coloneqq{u\in S,v\in V\setminus S}$ is in some MST of $G$.
UnionFind data structure of vertices.sort() if $W$ is int-valued and using Radix Sort.UnionFind.connected() and UnionFind.union(), which can be amortized $Θ(\alpha(V))$.def GetMinSpanTreeByKruskal(vertices, edges, get_weight):
# Initialization:
mst = set() # edges
uf = UnionFind(vertices) # one component for each vertex
sort(edges, get_weight) # may be linear
# Greedily choose the lowest-weight edge:
for (u, v) in edges:
if not uf.connected(u, v):
uf.union(u, v)
mst.add((u, v))
# Termination:
return mst
LeetCode
MinPQ on $V\setminus S$, where $d(S, v)\coloneqq\min_{u\in S}{W(u, v)}$ is used as $v$’s key.MinPQ.pop_min()MinPQ.change_key(), which can be amortized $Θ(1)$ if using Fibonacci Heap.def GetMinSpanTreeByPrim(vertices, edges, get_weight):
# Initialization:
mst = dict() # vertex to parent
pq = MinPQ() # v.key := d(S, v)
for v in vertices:
v.parent = None
v.key = float('inf')
pq.add(v)
# Choose the root (arbitrarily):
u = pq.pop_min()
mst[u] = None
for v in u.neighbors:
v.key = get_weight(u, v) # float up in the MinPQ
v.parent = u
# Greedily choose the next (V-1) vertices:
while len(pq):
u = pq.pop_min()
mst[u] = u.parent
for v in u.neighbors:
if (v not in mst) and (get_weight(u, v) < v.key):
pq.change_key(v, key=get_weight(u, v))
v.parent = u
# Termination:
return mst
def find_shortest_path(source, graph, get_weight):
# Initialization:
vertex_to_length = dict()
vertex_to_parent = dict()
for v in graph.vertices:
vertex_to_length[v] = float('inf')
vertex_to_parent[v] = None
vertex_to_length[source] = 0
# Relaxation:
while True:
u, v = _select_edge(graph) # return (None, None) if
# for all (u, v), there is d[v] <= d[u] + w(u, v).
if u is None:
break # go to the termination step
d = vertex_to_length[u] + get_weight(u, v)
if vertex_to_length[v] > d: # need relaxation
vertex_to_length[v] = d
vertex_to_parent[v] = u
# Termination:
return vertex_to_length, vertex_to_parent
MinPQ.insert(Vertex, Key)MinPQ.pop_min()MinPQ.decrease(Vertex, Key), which can be amortized $Θ(1)$ if using Fibonacci Heap.def find_shortest_path(source, graph, get_weight):
# Initialization:
unfinished_vertices = MinPQ()
vertex_to_length = dict()
vertex_to_parent = dict()
for v in graph.vertices:
unfinished_vertices.insert(v, float('inf'))
vertex_to_length[v] = float('inf')
vertex_to_parent[v] = None
unfinished_vertices.decrease(source, 0)
vertex_to_length[source] = 0
# Relaxation:
while len(unfinished_vertices):
u = unfinished_vertices.pop_min()
for v in u.neighbors:
d = vertex_to_length[u] + get_weight(u, v)
if vertex_to_length[v] > d: # need relaxation
unfinished_vertices.decrease(v, d)
vertex_to_length[v] = d
vertex_to_parent[v] = u
# Termination:
return vertex_to_length, vertex_to_parent
In practice, the decrease() operation may be replaced by a insert() operation, which inserts a new copy of the Vertex with a decreased Key. The deletion of the old copy is delayed or even skipped.
# no-decreasing version
def find_shortest_path(source, graph, get_weight):
# Initialization:
unfinished_vertices = MinPQ()
finished_vertices = set()
vertex_to_length = dict()
vertex_to_parent = dict()
for v in graph.vertices:
unfinished_vertices.insert(v, float('inf'))
vertex_to_length[v] = float('inf')
vertex_to_parent[v] = None
unfinished_vertices.insert(source, 0)
vertex_to_length[source] = 0
# Relaxation:
while len(finished_vertices) < len(graph.vertices):
u = unfinished_vertices.pop_min()
if u not in finished_vertices:
for v in u.neighbors:
d = vertex_to_length[u] + get_weight(u, v)
if vertex_to_length[v] > d: # need relaxation
unfinished_vertices.insert(v, d)
vertex_to_length[v] = d
vertex_to_parent[v] = u
finished_vertices.insert(u)
# Termination:
return vertex_to_length, vertex_to_parent
LeetCode
relax():def find_shortest_path(source, graph, get_weight):
for i in range(len(graph.vertices) - 1):
for u, v in graph.edges:
relax(u, v, get_weight(u, v))
# One more pass to find negative cycles:
for u, v in graph.edges:
if relaxable(u, v, get_weight(u, v)):
raise Exception("There exists a negative cycle!")
relax():def find_shortest_path(source, graph, get_weight):
sorted_vertices = topological_sort(graph)
for u in sorted_vertices:
for v in graph.get_neighbors(u):
relax(u, v, get_weight(u, v))
LeetCode
对于只含非负边的图,可以对每个点调用 Dijkstra。
以下算法适用于含负边、但不含负环的图。
令 \(l_{ij}^{(r)}\) 表示 \(i\to j\) 至多含 \(r\) 条边的最短路径,则初始值
\[l_{ij}^{(0)}= \begin{cases} 0,&i=j,\\ \infty,&i=j,\\ \end{cases}\]递归地有
\[l_{ij}^{(r)}=\min_{k=1}^{V}\qty(l_{ik}^{(r-1)}+w_{kj}),\]\(\forall r\) 有 \(V\times V\) 个值需要更新,故整体时间复杂度为 \(\order{V^4}\).
类比矩阵乘法,有如下对应关系:
| 矩阵乘法 | 最段路径 |
|---|---|
| \(c_{ij}=\sum_{k=1}^{V}a_{ik}\cdot b_{kj}\) | \(l_{ij}^{(r)}=\min_{k=1}^{V}\qty(l_{ik}^{(r-1)}+w_{kj})\) |
| \(a\) | \(l^{(r-1)}\) |
| \(b\) | \(w\) |
| \(c\) | \(l^{(r)}\) |
| \(\sum\) | \(\min\) |
| \(\cdot\) | \(+\) |
故最短路径问题归结为矩阵乘幂:
\[L^{(r)}=L^{(r-1)}\cdot W=\cdots=W^{r},\]利用分治策略,时间复杂度可降为 \(\order{V^3\lg V}\).
令 \(d_{ij}^{(k)}\) 表示中间节点只含 \(1,\dots,k\) 的最短路径,则初值及递归式分别为
\[d_{ij}^{(k)}= \begin{cases} w_{ij},&k=0\\ \min\qty(d_{ij}^{(k-1)},d_{ik}^{(k-1)}+d_{kj}^{(k-1)}),&k>0,\\ \end{cases}\]\(\forall k\) 有 \(V\times V\) 个值需要更新,故整体时间复杂度为 \(\order{V^3}\).
对于稀疏图,可以先用 Bellman–Ford 改造为只含非负边的图,再用对每个 vertex 调用 Dijkstra,故整体时间复杂度为 \(\order{V^2\lg V+VE}\).
图的改造方法如下:
在 \(G\) 外引入一点 \(s\),令 \(\forall v\in V : w(s,v)=0\),用 Bellman–Ford 得到 \(\delta(s,v)\),记作 \(h(v)\)。
由最短路径的三角不等式性质可以得到:
\[w(u,v)+h(u)-h(v)\ge0\impliedby\delta(s,v)\le\delta(s,u)+w(u,v).\]| \(\hat{G}\) | \((\hat{V},\hat{E})\) |
|---|---|
| \(\hat{V}\) | \(V\cup{s}\) |
| \(\hat{E}\) | \(E\cup\{(s,v):v\in V\}\) |
| \(\hat{w}(u,v)\) | \(w(u,v)+h(u)-h(v)\) |
| \(\hat{\delta}(u,v)\) | \(\hat{\delta}(u,v)=\delta(u,v)+h(u)-h(v)\) |